使用 Collections.sort() 对 ArrayList 数组进行排序时,偶现了 IllegalArgumentException 异常,于是追根溯源,对使用的排序算法-TimSort,出现异常的原因及其解决方案进行了如下的总结。
在灰度期间,上报了一个排序的 bug,如下所示:
1 | java.lang.IllegalArgumentException: Comparison method violates its general contract! |
定位到业务代码,实现的比较器如下:
1 | Collections.sort(list, new Comparator<Integer>() { |
跟踪系统实现排序的地方,在 JDK 7 中,对比较器的实现做了比较严格的限制,当俩个值相等(o1 = o2)时,需要保证 compare(o1, o2) = 0 ,而在 JDK 6 使用时是没问题的。为了一探究竟,就定位到了实现 sort 算法的位置:
1 | public static <T> void sort(T[] a, Comparator<? super T> c) { |
JDK ≥ 7 在这里更新了排序算法,如果指定了 LegacyMergeSort.userRequested 值为 true,则使用老的 ( JDK < 7)mergeSort;如果没有指定,则使用 TimSort。老的归并排序没有产生过这种异常,那为什么 Java 竟然会放弃兼容,替换成 TimSort 后会异常呢?接下来我们先深入 TimSort 的排序原理,再来看看出错的原因及其解决方案。
TimSort 原理
TimSort 结合了归并排序(merge sort)和插入排序(insertion sort),它基于一个简单的事实:大部分数据都是部分有序的。Youtube 上有一个很直观的 TimSort 排序视频:https://www.youtube.com/watch?v=NVIjHj-lrT4,可以通过这段视频对算法的过程有一个感性的了解。
TimSort 算法定义数组中一个有序的片段为 run,每个 run 都要求严格升序或降序,来保证算法的稳定性,如下所示:
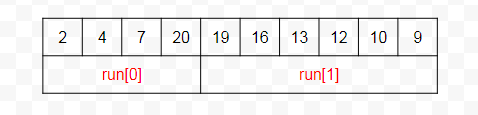
划分 run
TimSort 首先将待排序的数组,按照严格升序或降序(保证算法稳定性)划分一段一段的 run,如果为逆序则进行翻转,但是它的长度不能小于 minRun 这个阈值;如果长度小于 minRun,则把之后的数按照二分查找插入到该区间直到满足最小的长度要求。
这里我们定义一组待排序的数列:

假设最小的 run 长度为 minRun = 4 ,则上述待排序数组可以分为以下不同的 run 区间:
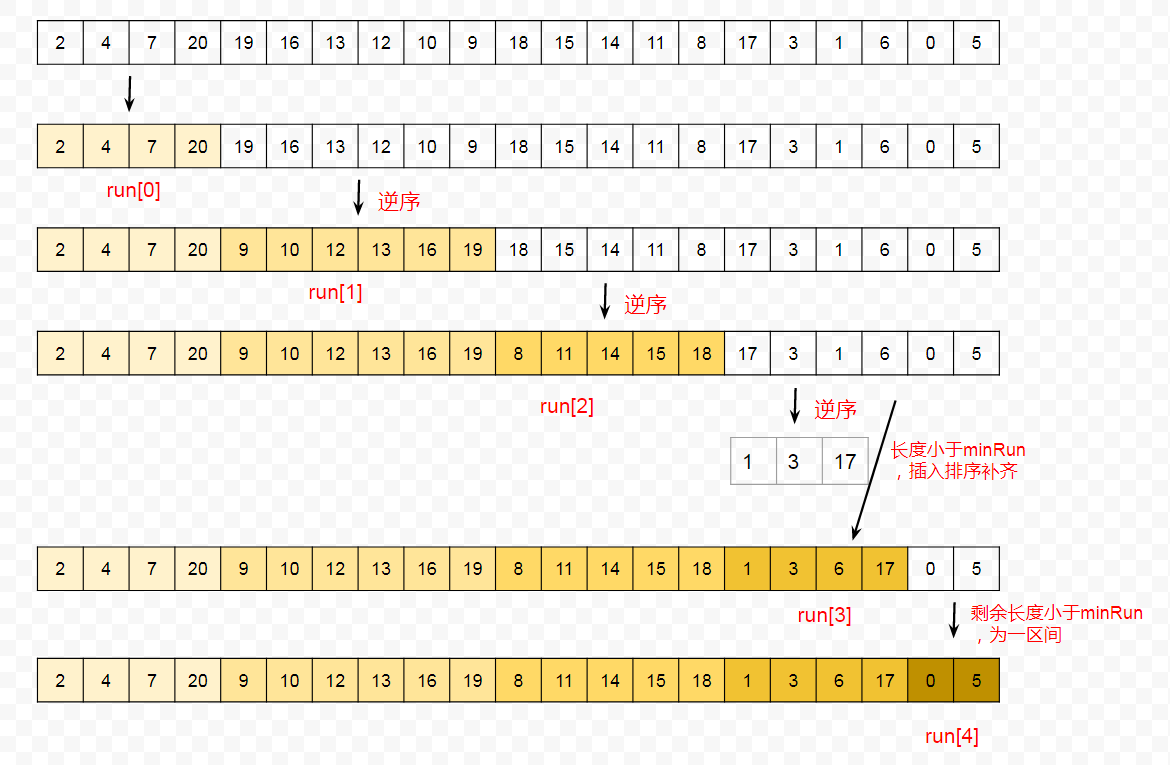
- 如果该数组是一个完全正序或逆序的,则只需要划分一个 run,这时排序只需要 O(N) 的时间。
- 划分过程中,如果长度小于 minRun,则会把后边的数按照二分查找算法插入补齐,如果是最后剩余的部分,则单独组成一个 run。
run 合并
TimSort 第二步就是对划分的 run 进行压栈,对于在栈顶的 run[i],必须同时满足以下条件:
1 | 1. runLen[i - 2] > runLen[i - 1] + runLen[i] |
如果有一个不满足,则会把最短的 2 个 run 进行归并成一个新的 run。接下来看看上述待排序的数组是如何把 run 进行合并的。
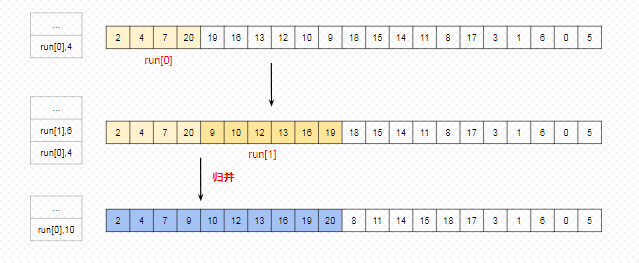
当把 run[1] 压栈时,可以看到 runLen[0] < runLen[1] ,所以需要把俩个 run 进行归并,合成一个新的 run 再重新压入栈中。
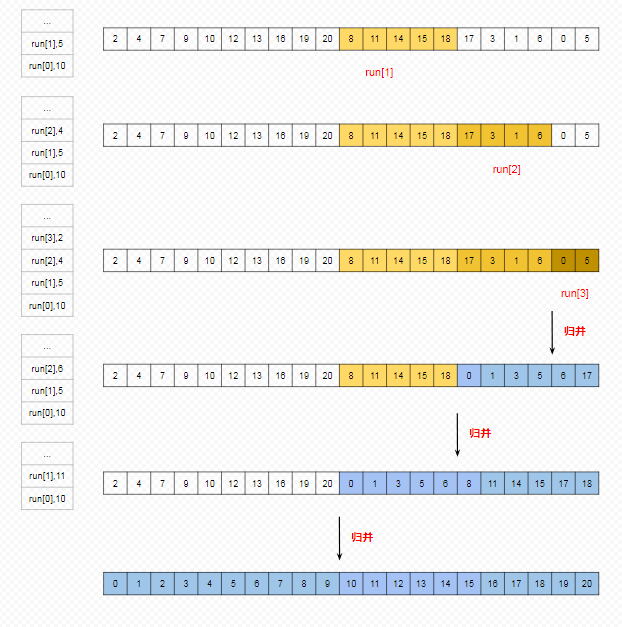
之后我们一次把 run[1](10 > 5),run[2](10>5+4 & 5>4)入栈,因为在栈顶的 run 都满足约束条件。当把 run[3] 入栈时,发现 runLen[1] > runLen[2] + runLen[3] 不成立,所以需要把 run[3] 和 run[2] 合并。之后也仍然按照这样的规则进行,当栈空时,也就排好序了。
俩个 run 的归并排序
TimSort 把 run 压人栈顶,如果不满足俩个约束条件,会把较短的俩个 run 进行归并排序,这里的归并排序相对普通的归并做了俩个优化点,都是充分利用一个简单的事实:大部分数据都是部分有序的。
Galloping Mode 减少参与归并的数据
假若有以下俩个 run ,不满足约束条件需要进行合并。设 run[0] 别称为 A,首地址为 base1,长度为 len1;run[1] 别称为 B,首地址为 base2,长度为len2。
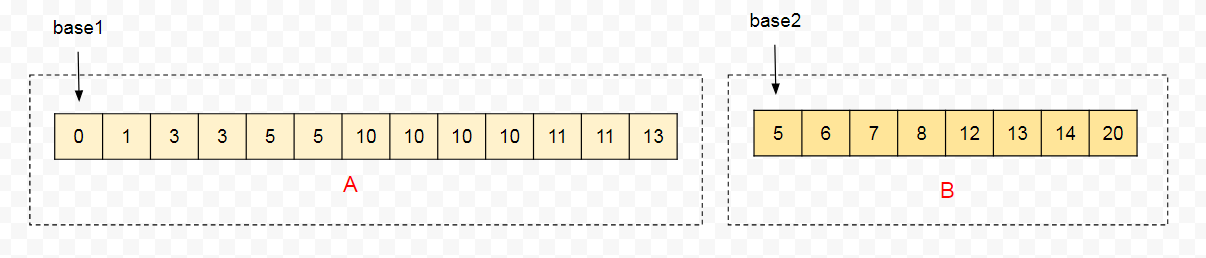
在 Galloping Mode 下,会根据以下条件查找对应区间:
- 取 B 片段的起始值 B[base2],在 A 片段中使用二分查找,则 A 片段中小于等于 B[base2] 段就是最终排好序的起始部分。
- 取 A 片段的终点值 A[base1 + len1 - 1],在 B 片段中进行二分查找,则 B 片段中大于等于 A[base1 + len1 - 1] 的区间就是最终归并排序的结束部分。
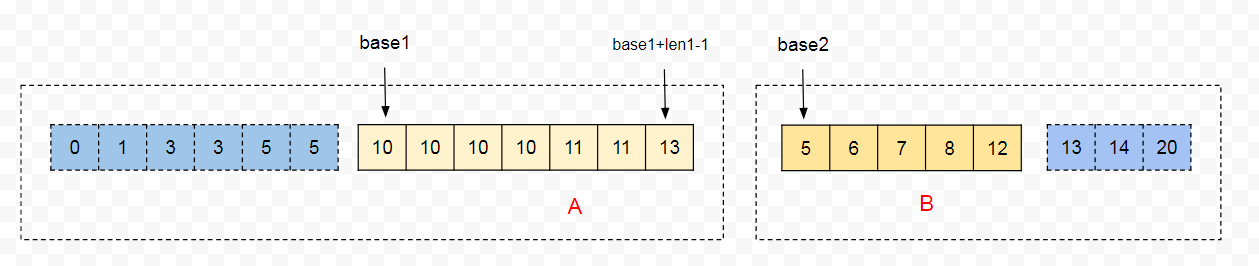
这里充分利用了部分数据有序这个事实,形象的“掐头去尾”,这样最终需要归并的数据只有中间的俩段数据。
连续胜利 MIN_GALLOP 次继续触发 Galloping
对 A 和 B 的俩个剩余片段,添加俩个指针,cursor1 指向 A 片段的末尾 cursor1 = base1 + len1 - 1 ,dest 指向 B 的剩余片段的末尾 dest = base2 + len2 - 1 。
因为在上一步骤中保证了 A [cursor1] > B[dest],所以会先把 A 片段的最后一个数据直接拷贝到 B 片段的末尾,同时 cursor--,dest-- 。
剩余的俩段区间,选择长度较小的一段复制到临时的 tmp 数组(节省内存开销),这里 B 片段的区间小一点,所以会放到临时数组的是 B 的剩余归并片段。
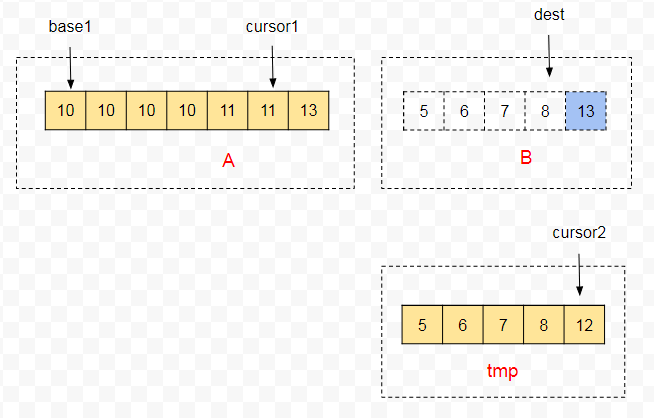
接着对 A 片段和 tmp 片段做普通的归并,A[cursor1] 和 tmp[cursor2] 进行比较,把比较大数移到 A[dest],同时 dest 和对应片段的指针减1。
在俩个片段的比较过程中,会记录 A 片段和 tmp 片段比较胜利(大于对方)次数,比较失败会直接把胜利次数清零。当某个片段的胜利次数大于 minGallop ,会进一步触发 Galloping 。假设 minGallop = 4 ,则 A 片段在胜利 4 次后会如下图所示,
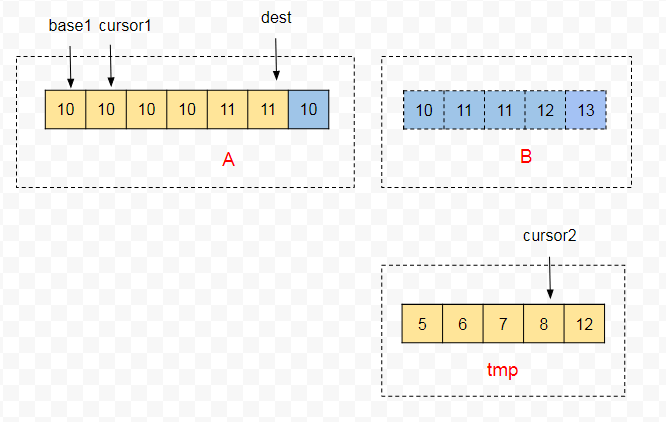
触发 Galloping
取 tmp 片段的终点值 tmp[cursor2],在 A 片段中二分查找到小于 tmp[cursor2] 的索引 k,则 A[k + 1, cursor1] 这个片段都大于 tmp[cursor2],这时就可以直接把 A[k + 1, cursor1] 复制到 A[dest - len, dest](len = cursor1 - k + 1)。如图找到的 k = -1 ,把俩个 10 复制过去后,cursor1 就到了 k 的位置了。
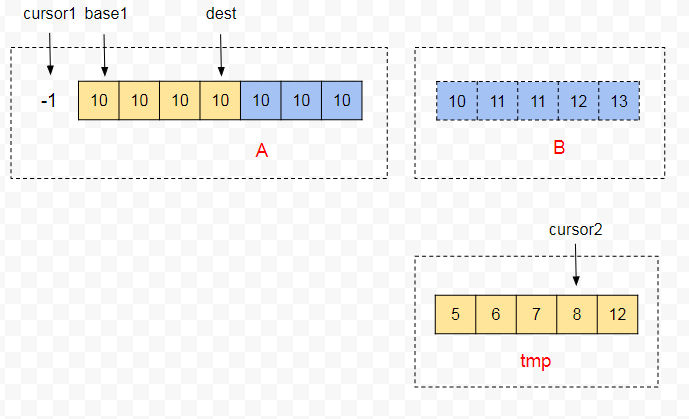
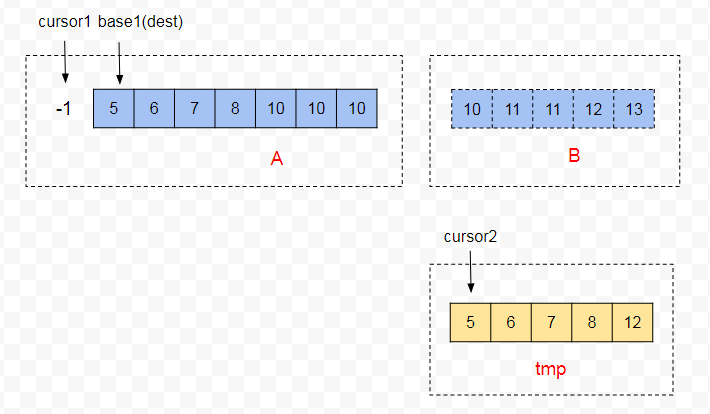
如果 cursor1 >= 0 ,俩个片段会继续进行归并比较,当连胜 minGallop 次才会又一次出发 Galloping。这里 cursor1 = -1 ,所以接下来只要把tmp 剩余的数据拷贝到 A[base1, dest] 即可。
总结
TimSort 排序算法综合了折半插入(二分查找)排序和归并排序,侧重优化了部分数据有序的情况,减少了对升序部分的回溯和对降序部分的性能倒退(快速排序在有序的情况下会退化到O(N^²))。其算法思路总结如下
- 当待排序数组长度小于 MIN_MERGE(
MIN_MERGE = 32),会使用没有归并的 TimSort,也就是会先进行一次 Galloping 找到左边有序的一个片段,再对后边的数据进行二分查找(折半插入)排序。 - 划分长度不小于 minRun 且严格升序(降序则翻转,不足则用后边数据二分查找插入)的 run 片段,并压人栈中,当不满足约束条件时,进行归并
- 在归并过程中,会先进行 Galloping,“掐头去尾”,再进行中间俩个片段的归并
- 俩个片段比较过程中,若某个片段连胜 MIN_GALLOP,则又会进行一次 Galloping,进行”掐头” 或“去尾”,否则就退化成普通的归并排序。
TimSort 的时间和空间复杂度如下表:
| Algorithm | Average | Best | Worst | extra space | stable |
|---|---|---|---|---|---|
| TimSort | O(NlogN) | O(N) | O(NlogN) | O(N) | 稳定 |
在完全正序或逆序的情况下,TimSort 只需要 O(N) 的时间和 O(1) 的空间,空间消耗主要来自于俩个片段归并过程中创建的临时数组。
出错原因
回到在业务中使用 Collections.sort() 时,当 Comparator 没有实现俩个数据相等情况下返回 0 的情况下,会出现 IllegalArgumentException。假设这里实现的比较器如下:
1 | new Comparator<Inteager>() { |
则当 o1 = o2 时,有如下等式成立:
- compare(o1,o2) < 0
- compare(o2,o1) < 0
这里我们假设现在有俩个 run 需要进行归并:
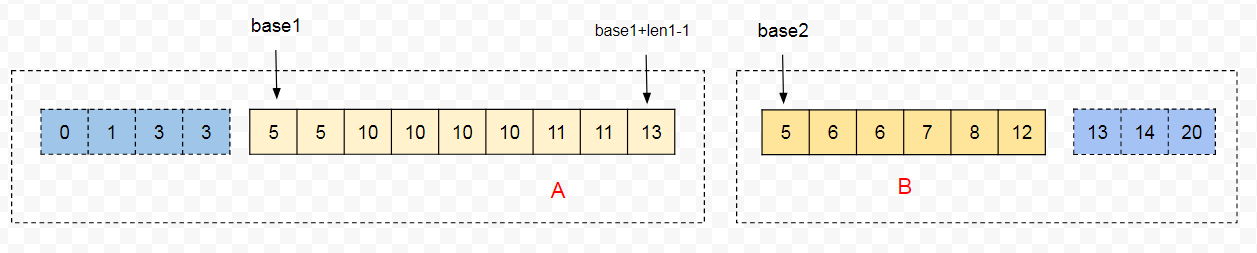
1、在进行 Galloping “掐头” 过程中,执行 compare(B[base2], A[base1 + hint]) 过程中,因为 compare(o1,o2) < 0 (o1 = o2),所以此时 B 片段中的 5 是比 A 片段中的俩个 5 都要小,所以 A 片段的 5 都会保留下来。
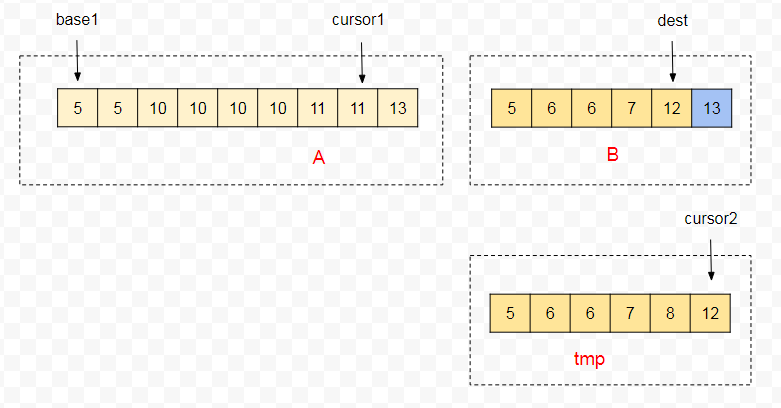
之后中间俩个片段进行正常的归并,当连胜 minGallop(minGallop = 4)次后会又一次触发 Galloping。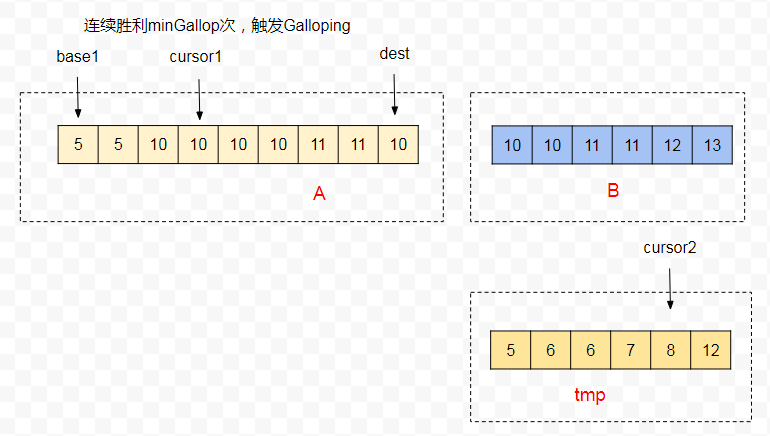
2、在这次 Galloping 中,会在 A 片段中查找比 tmp[cursor2] 还要小的位置 k,并把 A[K + 1, cursor1] 移到 A[dest - len, dest] 中,同时 cursor1 和 dest 左移俩位。
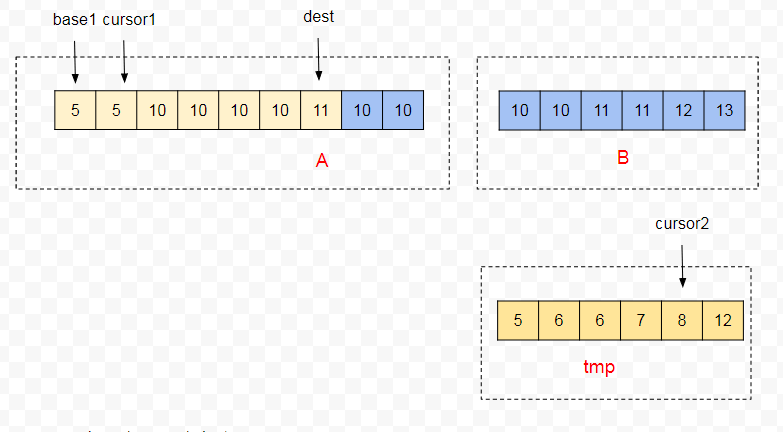
3、接下来俩个片段在归并过程中,tmp[cursor2] 连续 4 次比 A[cursor1] 大,又一次触发 Galloping。
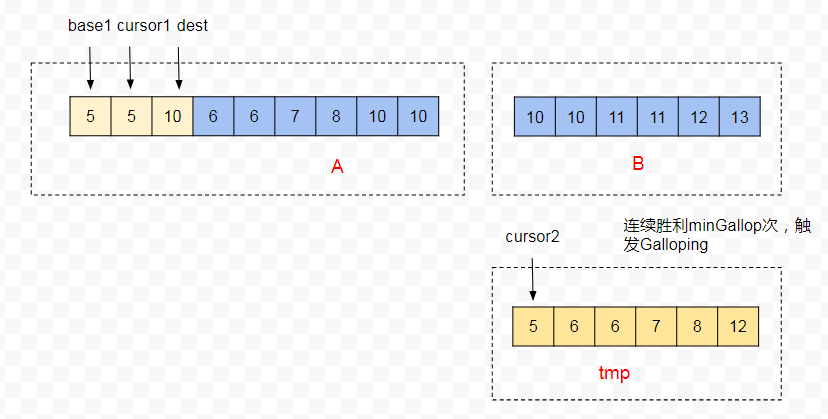
4、在这次 Galloping过程中,取 A 片段的 A[cursor1] 的值,去 tmp 片段中查找大于 A[cursor1] 的区间。使用比较器 compare(A[cursor1],tmp[k]),因为 compare(o1,o2) < 0 (o1 = o2),所以此时 A 片段中的 5 是小于 tmp 片段中的 5。tmp 的数据会依次拷贝到 A[dest] 后,cursor2的指针到-1了,且此时 tmp 数组的长度 len2 为 0。
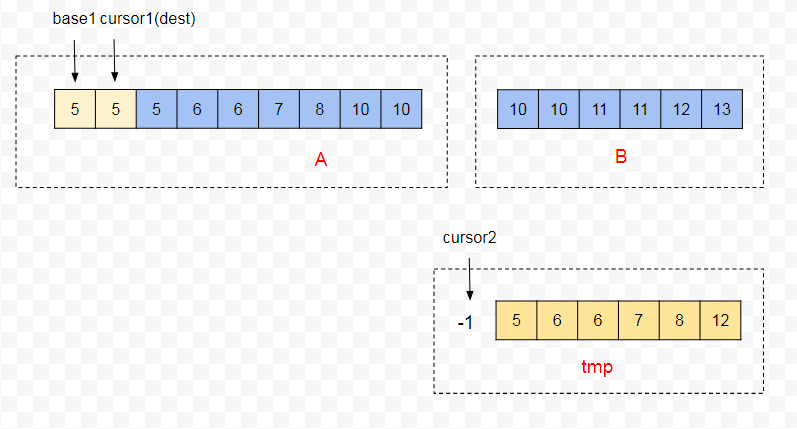
5、因为 tmp 的长度(len2)为 0,会触发 mergeHi 中如下的异常
1 | } else if (len2 == 0) { |
我们再回顾一下上边的过程,在第 1 步“掐头去尾”中,我们保证 A[base1] > B[base2],在第 4 步中,cursor2 最终指到 -1 了,所以有 A[cursor1] < tmp[0],即:A[base1 + 1] < B[base2]。综上可以列出以下等式:
- A[base1] <= A[base1 + 1]
- A[base1] > B[base2]
- A[base+1] < B[base2]
A[base1] <= A[base1+1]<B[base2]<A[base1],显然不合情理。
从另一个角度来看:在 mergeHi 中把后边的 B 片段取出放到临时数组 tmp 里,B 片段的第一个数据 B[base2] 肯定是最后一个才会放进去的,因为把小于 B[base2] 的数据第一步就掐走了,在留下的 A 片段里肯定都是不小于 B[base2] 的数据。
因为不满足比较器的自反性(compare(o1, o2) ≠ compare(o2 , o1),if o1 = o2),当有相等的值,且俩个片段在进行 Galloping 时正好用了俩次 compare(一次 compare(o1, o2),一次compare(o2, o1)),这时便有可能会触发这个异常。
解决方案
经过对 TimSort 源码及出错的原因分析,我们可以很快的得到如下俩种解决方案。
严格实现比较器
在创建比较器 Comparator 实现 compare() 方法中,当俩个值相等(o1 = o2)时,必须保证 compare(o1, o2) = 0 。
使用旧的排序算法
JDK 6 及以下的版本中,使用的排序算法是普通的归并排序,不需要 compare(o1, o2) = 0(o1 = o2) 这么严格的条件。所以第二种解决方法仍然使用老版本的归并排序算法,设置如下:
1 | System.setProperty("java.util.Arrays.useLegacyMergeSort", "true"); |
